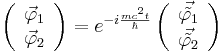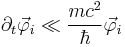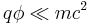Pauli equation

Quantum mechanics
$\Delta x\, \Delta p \ge \frac{\hbar}{2}$ Uncertainty principle
Introduction Glossary · History
Background Bra-ket notation · Classical mechanics Hamiltonian · Interference Old quantum theory
Fundamental concepts Complementarity · Decoherence Duality · Ehrenfest theorem Entanglement · Exclusion Measurement · Probability amplitude Nonlocality · Quantum state Superposition · Tunnelling Uncertainty · Wave function
Experiments Bell's inequality · Davisson–Germer Delayed choice quantum eraser Double-slit · Elitzur–Vaidman Popper · Quantum eraser Schrödinger's cat · Stern–Gerlach Wheeler's delayed choice
Formulations Formulations Heisenberg · Interaction Matrix mechanics · Schrödinger Sum over histories
Equations Dirac · Klein–Gordon Pauli · Rydberg Schrödinger
Interpretations Consciousness-caused Consistent histories Copenhagen · de Broglie–Bohm Ensemble · Hidden variables Many-worlds · Objective collapse Pondicherry · Quantum logic Relational · Stochastic Transactional
Advanced topics Quantum chaos · Quantum field theory Quantum information science Scattering theory
Scientists Bell · Bohm · Bohr · Born · Bose de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner

The Pauli equation, also known as the Schrödinger–Pauli equation, is the formulation of the Schrödinger equation for spin-¹⁄₂ particles which takes into account the interaction of the particle's spin with the electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are slow enough that relativistic effects can be neglected.

It was formulated by Wolfgang Pauli in 1927.^[1]

1 Details
2 Relationship to the Schrödinger equation and the Dirac equation
3 Special Cases
4 Derivation of the Pauli equation by Schrödinger
5 References
6 Notes and references

Details

The Pauli equation is stated as:

$\left[ \frac{1}{2m}(\vec{\sigma}\cdot(\vec{p} - q \vec{A}))^2 %2B q \phi \right] |\psi\rangle = i \hbar \frac{\partial}{\partial t} |\psi\rangle$

where:

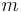$m \ \$ is the mass of the particle.
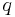$q \ \$ is the charge of the particle.
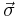$\vec{\sigma} \ \$ is a three-component vector of the two-by-two Pauli matrices. This means that each component of the vector is a Pauli matrix.
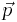$\vec{p} \ \$ is the three-component vector of the momentum operators. The components of this vector are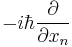 $- i \hbar \frac{\partial}{\partial x_n}$
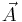$\vec{A} \ \$ is the three-component magnetic vector potential.
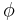$\phi \ \$ is the electric scalar potential.
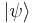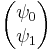$|\psi\rangle \ \$ is the two component spinor wavefunction, which can be represented as $\begin{pmatrix} \psi_0 \\ \psi_1 \end{pmatrix}$ .

Somewhat more explicitly, the Pauli equation is:

$\left[ \frac{1}{2m} \left( \sum_{n=1}^3 \left(\sigma_n \left( - i \hbar \frac{\partial}{\partial x_n} - q A_n\right)\right) \right) ^2 %2B q \phi \right] \begin{pmatrix} \psi_0 \\ \psi_1 \end{pmatrix} = i \hbar \begin{pmatrix} \frac{\displaystyle \partial \psi_0 }{\displaystyle \partial t} \\[6pt] \frac{\displaystyle \partial \psi_1 }{\displaystyle \partial t} \end{pmatrix}$

Notice that the Hamiltonian (the expression between square brackets) is a two-by-two matrix operator, because of the Pauli $\sigma$ matrices.

Relationship to the Schrödinger equation and the Dirac equation

The Pauli equation is non-relativistic, but it does predict spin. As such, it can be thought of an occupying the middle ground between:

The familiar Schrödinger equation (on a complex scalar wavefunction), which is non-relativistic and does not predict spin.
The Dirac equation (on a complex four-component spinor), which is fully relativistic (with respect to special relativity) and predicts spin.

Note that because of the properties of the Pauli matrices, if the magnetic vector potential 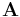$\bold{A}$ is equal to zero, then the equation reduces to the familiar Schrödinger equation for a particle in a purely electric potential $\phi$ , except that it operates on a two component spinor. Therefore, we can see that the spin of the particle only affects its motion in the presence of a magnetic field.

Special Cases

Both spinor components satisfy the Schrödinger equation. This means that the system is degenerated as to the additional degree of freedom.

With an external electromagnetic field the full Pauli equation reads:

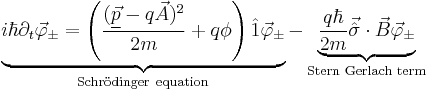$\underbrace{i \hbar \partial_t \vec \varphi_\pm = \left( \frac{(\underline{\vec p}-q \vec A)^2}{2 m} %2B q \phi \right) \hat 1 \vec \varphi_\pm}_\mathrm{Schr\ddot{o}dinger~equation} - \underbrace{\frac{q \hbar}{2m}\vec{\hat \sigma} \cdot \vec B \vec \varphi_\pm}_\text{Stern Gerlach term}$ .

where

$\phi$ is the scalar electric potential

$A$ the electromagnetic vector potential

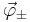$\vec \varphi_\pm$ , in Dirac notation 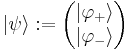$|\psi\rangle�:=\begin{pmatrix} |\varphi_%2B\rangle \\ |\varphi_-\rangle \end{pmatrix}$ , are the Pauli spinor components

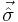$\vec{\hat \sigma}$ are the Pauli matrices

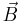$\vec B$ is the external magnetic field

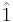$\hat 1$ two dimensional Identity matrix

The Stern–Gerlach term can obtain the spin orientation of atoms with one valence electron, e.g. silver atoms which flow through an inhomogeneous magnetic field.

Analogously, the term is responsible for the splitting of spectral lines (corresponding to energy levels) in a magnetic field as can be viewed in the anomalous Zeeman effect.

Derivation of the Pauli equation by Schrödinger

Starting from the Dirac equation for weak electromagnetic interactions:

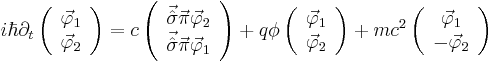
$i \hbar \partial_t \left( \begin{array}{c} \vec \varphi_1\\\vec \varphi_2\end{array} \right) = c \left( \begin{array}{c} \vec{\hat \sigma} \vec \pi \vec \varphi_2\\\vec{\hat \sigma} \vec \pi \vec \varphi_1\end{array} \right)%2Bq \phi \left( \begin{array}{c} \vec \varphi_1\\\vec \varphi_2\end{array} \right) %2B mc^2 \left( \begin{array}{c} \vec \varphi_1 \\-\vec \varphi_2\end{array} \right)$

with 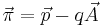$\vec \pi = \vec p - q \vec A$

using the following approximations:

Simplification of the equation through following ansatz

$\left( \begin{array}{c} \vec \varphi_1 \\ \vec \varphi_2 \end{array} \right) = e^{-i \frac{mc^2t}{\hbar}} \left( \begin{array}{c} \vec{\tilde{\varphi_1}} \\ \vec{\tilde{\varphi_2}} \end{array} \right)$

Eliminating the rest energy through an Ansatz with slow time dependence

$\partial_t \vec \varphi_i \ll \frac{mc^2}{\hbar} \vec \varphi_i$

weak coupling of the electric potential

$q \phi \ll mc^2$

References

Schwabl, Franz (2004). Quantenmechanik I. Springer. ISBN 978-3540431060.
Schwabl, Franz (2005). Quantenmechanik für Fortgeschrittene. Springer. ISBN 978-3540259046.
Claude Cohen-Tannoudji, Bernard Diu, Frank Laloe (2006). Quantum Mechanics 2. Wiley, J. ISBN 978-0471569527.

Notes and references

^ Wolfgang Pauli (1927) Zur Quantenmechanik des magnetischen Elektrons Zeitschrift für Physik (43) 601-623